6.4.1. הבעיה והאלגוריתםבדיקת מודל מפורשת (Explicit model checking) היא אלגוריתם המבצע בדיקת מודל, העובד ישירות על הגרף - מבנה קריפקה. המודל M נתון באופן מפורש כייצוג של הגרף – וממומש לרוב כמטריצת סמיכויות או כרשימת בנים. האלגוריתם המפורש הוא קל להבנה, אך
בעייתי למימוש עקב "בעיית התפוצצות המצבים": במערכת בה כדי לפתור את בעיה זו נציג בהמשך 2 אלגוריתמים אחרים שהם אלגוריתמים סימבוליים – אנו נציג קידוד של המבנה M וגם של תוצאות הביניים המאפשר שימוש בפחות זכרון. האלגוריתם לבדיקת מודל CTL מטפל בנוסחאות מהצורה: תיאור כללי של האלגוריתם: נצרף לכל מצב
האלגוריתם עובד באיטרציות על תתי
הקבוצות של דוגמא לסדר הטיפול: עבור הנוסחה הבאה
בעמודים הבאים נציג מה הפירוש של
"טיפול בתת נוסחה בכל איטרציה האלגוריתם לסימון: צעד 0: נוסחאות אטומיות לכל סיבוכיות:
צעד
זה הוא היחיד שלא קשור לנוסחה נסמן כל מצב בנוסחאות האטומיות המספקות אותו. צעד 1: סימון
ב- לכל
סיבוכיות: סימון
ב- לכל
סיבוכיות: סימון
ב- לכל מצב
פירוש: קיימת קשת מצומת האב לצומת אחר,
וגם מתקיים סיבוכיות האלגוריתם לסימון
ניסוח חלופי לאלגוריתם צעד-צעד להבהרת הפעולה:
האלגוריתם
מסתמך על השקילות הבאה: סיבוכיות האלגוריתם: הערות על האלגוריתם:
דוגמא:
שלב ראשון: מסומנים
ב- שלב שני: האבות
שלהם: אנחנו לא מסמנים את שלב שלישי: האבות
של האבות: אנו לא מסמנים ולא מטפלים שוב במצבים
שכבר סומנו ( ולבסוף: מתקבל בסוף:
האלגוריתם
לסימון הגדרות: רכיב קשיר היטב: (SCC) – Strongly Connected Component הינו תת גרף C, שבו מכל צומת יש מסלול לכל צומת ב-C, דרך צמתים ב-C.
דוגמא:
האלגוריתם של Tarjan
מוצא את כל הרכיבים המקסימאליים בסיבוכיות נגדיר את המבנה המצומצם הבא: בהינתן
נסתמך על המשפט הבא: משפט:
המשפט מבטיח לנו שקיים מסלול אינסופי בו
מסתפק האלגוריתם עצמו:
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


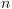 משתנים בוליאנים, יהיו
משתנים בוליאנים, יהיו 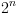 מצבים אפשריים למערכת. מספר
המצבים השונים גדל מהר מאוד כאשר המערכת גדלה, וכמות הזכרון לא מספיקה לייצוג מלא
של המודל.
מצבים אפשריים למערכת. מספר
המצבים השונים גדל מהר מאוד כאשר המערכת גדלה, וכמות הזכרון לא מספיקה לייצוג מלא
של המודל.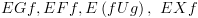 כאשר
כאשר 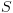 משתנה
משתנה 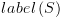 שיחזיק קבוצה של תתי נוסחאות
של
שיחזיק קבוצה של תתי נוסחאות
של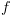 שנכונות ב-
שנכונות ב-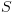 .
.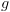 :
: 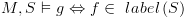
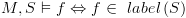 . נקבל את
. נקבל את 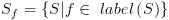 קבוצת המצבים שבהם הנוסחה נכונה.
קבוצת המצבים שבהם הנוסחה נכונה.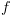 מהנוסחאות האטומיות אל הנוסחאות המורכבות יותר, על
כל תתי הקבוצות של
מהנוסחאות האטומיות אל הנוסחאות המורכבות יותר, על
כל תתי הקבוצות של 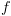 .
.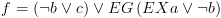
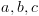
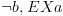
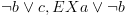
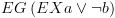
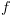
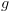 " שהוזכר בתיאור
האלגוריתם.
" שהוזכר בתיאור
האלגוריתם.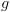 יהיה תת הנוסחה איתה אנו
מתעסקים.
יהיה תת הנוסחה איתה אנו
מתעסקים.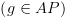
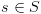 ,
, 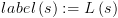 .
.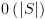
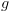 בה אנו מטפלים כרגע. בתחילת ריצת
האלגוריתם
בה אנו מטפלים כרגע. בתחילת ריצת
האלגוריתם 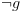
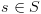 :
: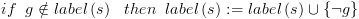
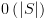
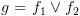
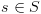 :
: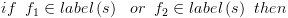
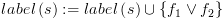
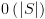
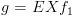
 :
: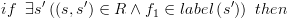
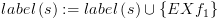
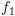 בצומת הבן.
בצומת הבן.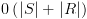
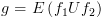
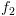 וסמנו אותם ב-
וסמנו אותם ב-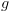 . נכניס את המצבים לקבוצה T ונסמן אותם כ-visit.
. נכניס את המצבים לקבוצה T ונסמן אותם כ-visit.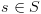 :
: ![plot:\[if\,\,{f_2} \in label\left( s
\right)\,\,\,then\,\]](/documentResources/326/plot_204.png)
![plot:\[label\left(
s \right): = label\left( s \right) \cup \left\{ g \right\}\]](/documentResources/326/plot_205.png)
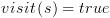
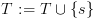
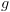 וסימון כל מצב שיש לו בן שמסומן ב-
וסימון כל מצב שיש לו בן שמסומן ב-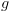 והוא עצמו מסומן ב-
והוא עצמו מסומן ב-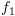 , ב-
, ב-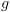 . אנו מבצעים סריקה אחורנית על מנת לא לסגור
מעגל.
. אנו מבצעים סריקה אחורנית על מנת לא לסגור
מעגל.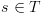 ונוציאו מ-
ונוציאו מ-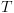 .
.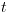 המקיים
המקיים 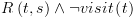 (
(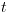 אב של
אב של  אותו עדיין לא ביקרנו), אם מתקיים
אותו עדיין לא ביקרנו), אם מתקיים 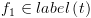 :
: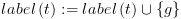
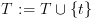
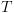 ריקה.
ריקה.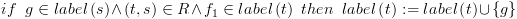
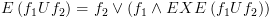
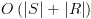
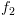 . (הסריקה האחורנית דואגת לכך).
. (הסריקה האחורנית דואגת לכך).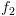 וגם מקיימים את התנאי.
וגם מקיימים את התנאי.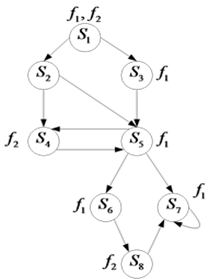
![plot:\[{f_2}\]](/documentResources/326/plot_206.png) :
: 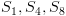 .
.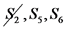
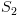 כי הוא אינו מסומן ב-
כי הוא אינו מסומן ב-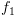 .
.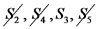
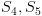 ).
).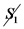
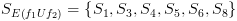
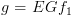
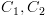 שניהם MSCC,
אזי
שניהם MSCC,
אזי 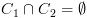 .
.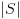 . סכום הצמתים ברכיבים קשירים היטב לא בהכרח
מקסימאליים הוא
. סכום הצמתים ברכיבים קשירים היטב לא בהכרח
מקסימאליים הוא 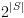 .
.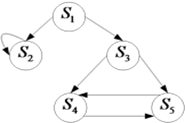
![plot:\[SCC = \left\{ {\left\{ 1 \right\},\left\{ 2 \right\},\left\{ 3
\right\},\left\{ 4 \right\},\left\{ 5 \right\},\left\{ {4,5} \right\},\left\{
{3,4,5} \right\}} \right\}\]](/documentResources/326/plot_207.png)
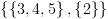
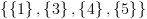 .
.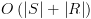 (כולל רכיבים טריויאליים).
(כולל רכיבים טריויאליים).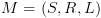 נגדיר
נגדיר 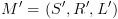 ע"י:
ע"י: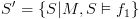
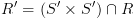 הערה:
הערה: 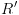 אינה בהכרח טוטאלית
אינה בהכרח טוטאלית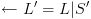 הטלה של
הטלה של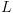 על
על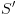
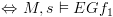
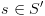
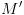 ממצב
ממצב למצב
למצב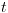 ברכיב קשיר היטב מקסימאלי לא טריוויאלי של
ברכיב קשיר היטב מקסימאלי לא טריוויאלי של 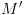 .
.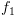 (ולא רק רישא סופית שבה הוא מסתפק).
(ולא רק רישא סופית שבה הוא מסתפק).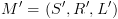 כמתואר לעיל.
כמתואר לעיל. 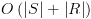
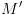 .
. 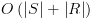
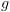 .
. 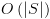
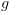 נבצע סקירה אחורנית ב-
נבצע סקירה אחורנית ב-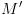 ונסמן כל מצב שממנו יש
מסלול לרכיב קשיר היטב.
ונסמן כל מצב שממנו יש
מסלול לרכיב קשיר היטב. 
 ושל
ושל 




