הרצאה 25 – גלים אלקטרומגנטיים, גל מישורי רץ, שטף האנרגיה של הגל האלקטרומגנטיגלים אלקטרומגנטיים
מקרה פרטי - גל מישורי רץ
תזכורת: משוואות מקסוול בריק
תכונות גלים א"מ מישוריים רצים נשתמש בפתרונת שאנו מציעים על מנת לקבל את תכונות הגלים האלקטרומגנטיים. ראשית, נציב את
מכאן כעת, נציב את תוצאה חשובה: גל אלקטרומגנטי הוא גל רוחבי. גם השדה החשמלי וגם השדה המגנטי ניצבים לכיוון ההתקדמות. נמשיך לחפש תכונות נוספות של הגל האלקטרומגנטי:
מסקנות: א. ב.
ניקח את הביטוי
ומכאן: שטף האנרגיה של הגל האלקטרומגנטי (ווקטור Poynting)
נבנה תיבה מקבילה לציר z. שטח החתך שלה יסומן A,
וגובהה יסומן כזכור, צפיפות האנרגיה הקשורה בשדות הינה: כמות האנרגיה האלקטרומגנטית
בתיבה שנפחה
נביט בביטוי המתמטי לנגזרת:
כאשר במקרה הפרטי, נכליל: מקרה פרטי הוא גל אלקטרומגנטי, ואז ווקטור
פוינטינג בכיוון התקדמות הגל הינו משמעות הווקטור: שטף האנרגיה בכיוון יחידות: מקרה פרטי - גל אלקטרומגנטי (מונוכרומטי) מישורי המקרה פרטי מכיוון ש-
תזכורת:
אנו נותנים כאן משמעות חדשה ל- החלק המגנטי של הגל:
ההבדל בין החלק החשמלי לחלק המגנטי: הערה: מרבית התופעות הפיסיקליות נובעות מהחלק החשמלי של השדה האלקטרומגנטי ולכן למרות ששני החלקים זהים בגודלים, בדרך כלל נדבר ונשתמש בנוסחאות בחלק החשמלי. ווקטור פוינטינג של הגל:
עוצמת הגל I: העוצמה I היא
למעשה הערך הממוצע של ווקטור הפוינטינג עבור גל מונוכרומטי:
הערה: עבור גל הרמוני מעגלי, העוצמה קטנה ב- הספק: ההספק המשודר הוא האינטגרל המשטחי של ווקטור פוינטינג הממוצע או באופן זהה של העוצמה. אנו מקבלים את ההספק הממוצע:
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |





 , כל הנקודות מקבלות את אותו ערך של הגל האלקטרומגנטי.
, כל הנקודות מקבלות את אותו ערך של הגל האלקטרומגנטי. היא אמפליטודת השדה החשמלי.
היא אמפליטודת השדה החשמלי.  היא אמפליטודת השדה המגנטי. עבור גל מישורי, שניהם קבועים.
היא אמפליטודת השדה המגנטי. עבור גל מישורי, שניהם קבועים.
 במשוואה
במשוואה  :
:

 , וכך נגיע אל התכונה הראשונה של גלים אלקטרומגנטיים:
, וכך נגיע אל התכונה הראשונה של גלים אלקטרומגנטיים:  .
. במשוואה
במשוואה  , ונקבל
, ונקבל  , ומכאן:
, ומכאן: 

 ומכאן
ומכאן  -
-  מהווים שלשה ימנית.
מהווים שלשה ימנית. . ל-
. ל- אותו גודל, וזאת מכיוון שמשוואות מקסוול סימטריות עבור
אותו גודל, וזאת מכיוון שמשוואות מקסוול סימטריות עבור  ועבור
ועבור  . מתקיים:
. מתקיים:  .
.



 , והוא מישורי כך ש-
, והוא מישורי כך ש- .
.
 . נבדוק את השינוי עם הזמן של
האנרגיה החשמלית והמגנטית בשטח זה.
. נבדוק את השינוי עם הזמן של
האנרגיה החשמלית והמגנטית בשטח זה. .
. :
:
 היא פונקציה של המקום ושל
הזמן, וזאת מכיוון שהשדות עצמם הם פונקציה של המקום ושל הזמן.
היא פונקציה של המקום ושל
הזמן, וזאת מכיוון שהשדות עצמם הם פונקציה של המקום ושל הזמן.

 הוא ווקטור Poynting:
הוא ווקטור Poynting:  - קצב שינוי אנרגיה ביחידת זמן ליחידת נפח בכיוון
ההתקדמות.
- קצב שינוי אנרגיה ביחידת זמן ליחידת נפח בכיוון
ההתקדמות. , מתקיים:
, מתקיים:  .
. .
.
 תמיד, והשדות שווים בגודלם בכל רגע (אם כי גודל זה משתנה).
תמיד, והשדות שווים בגודלם בכל רגע (אם כי גודל זה משתנה).

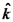 הוא כיוון התקדמות הגל,
הוא כיוון התקדמות הגל,  והתדירות היא
והתדירות היא  .
. : זהו ווקטור ההתקדמות של הגל.
: זהו ווקטור ההתקדמות של הגל.
 . מבחינת גודל:
. מבחינת גודל: 

 . ערך זה הוא ערך קבוע המתאר את עוצמת הגל.
. ערך זה הוא ערך קבוע המתאר את עוצמת הגל.
 , ועבור גל כדורי העוצמה יורדת לפי
, ועבור גל כדורי העוצמה יורדת לפי  .
.
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.