הרצאה 11 – מעגלים, חוק ג'אול, חוקי קירכהוף, תרגילים
מוליכים המקיימים את חוק אוהם
|
מוליך  בצורת גליל ישר, שטח חתך בצורת גליל ישר, שטח חתך  ובעל אורך L. ובעל אורך L.
נשתמש בחוק אום:  דרך שטח החתך A. דרך שטח החתך A.

|

|
דוגמא
נרצה לחשב את ההתנגדות של כדור מוליך מלא. המוליכות הסגולית
של הכדור היא  , והרדיוס שלו הוא
, והרדיוס שלו הוא  .
.
מתקיים:  .
.
ניקח קליפה כדורית דקה בעלת רדיוס r ונחשב את ההתנגדות שלה.

כעת dr הוא למעשה המרחק שעברנו כדי לחצות את הקליפה, ו- זהו השטח שלה.
זהו השטח שלה.
נבצע אינטגרל על מנת לקבל את כל הקליפה:

מודל Drude
המוליך מורכב מ- סוגים של נושאי מטען
סוגים של נושאי מטען  .
.
כמו כן המוליך מכיל מולקולות נטרליות שבהן מתנגשים נושאי
המטען.
משוואות התנועה לנושע מטען אחד מסוג j:
מהירות רגעית: 

תזכורת:
 הוא הממוצע של גודל פיסיקלי b:
הוא הממוצע של גודל פיסיקלי b: 
|
ממוצע המהירויות: |

|
נגדיר t=0 רגע ההתנגשות האחרונה של נושא המטען i,
ונגדיר  משך הזמן עד ההתנגשות הבאה.
משך הזמן עד ההתנגשות הבאה.
הזמן הממוצע בין התנגשויות עבור סוג j: 

ולכן אנו מקבלים כי:


כאשר  זוהי למעשה תכונה של החומר. נסמן:
זוהי למעשה תכונה של החומר. נסמן:  , ואז יתקיים כי:
, ואז יתקיים כי: 
חוק Joule
אנרגיה הופכת לחום בזמן הזרימה במוליך.
הספק הכוח החשמלי  הפועל על נושא מטען אחד:
הפועל על נושא מטען אחד:
כללית:  (כוח כפול מהירות).
(כוח כפול מהירות). 
הספק (חום) ליחידת נפח:

יחידות:
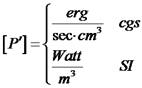
הספק החוק בקטע תיל מוליך:

נגדים
סימון ההתנגדות = נ?ג?ד

חיבור נגדים
|
חיבור טורי: |

|
|
מתקיים: |

|
|
חיבור במקביל: |

|
|
מתקיים: |

|
מעגלי זרם - חוקי קירהוף
- חוק המעגל:

- חוק הצומת:
מעגל זרם המכיל מקור כא"מ (כוח אלקטרו-מניע), קבל
ונגד
א. טעינת קבל

נפתור את המשוואה ההומוגנית:


פתרון פרטי של המשוואה האי הומוגנית:

סיכום:
טעינת קבל:

RC
נקרא קבוע הזמן של המעגל (ל-RC מימדים של זמן).
ב. פריקת קבל
|
ב- מתקיים: מתקיים:  . .
באותו רגע המפסק נסגר.
מתקיים:  |

|
|
העבודה המבוצעת בזמן טעינת הקבל על ידי מקור הכא"מ: |
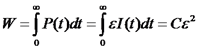
|
|
האנרגיה העצורה בקבל בסוף הטעינה: |

|
חוק Joule

נגד עם אלקטרודות בעלות צורה סימטרית
א. נגד כדורי
|
בין האלקטרודות תווך מוליך.
נתון:

כאשר  קבוע כלשהו. קבוע כלשהו. |

|
|
תכונת מוליך המקיים את חוק אום היא  , לכן: , לכן: |

|
| | |
ידוע כי 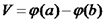 . נמצא את V בהתאם לנתוני השאלה:
. נמצא את V בהתאם לנתוני השאלה:

|
נשים לב כי ניתן להעלים את  מהמשוואה: מהמשוואה: |

|
|
הזרם הוא למעשה צפיפות הזרם כפול השטח, לכן:
קיבלנו מידע חשוב: הזרם אחיד ואינו תלוי ב-r!! |

|
מחוק אום ידוע לנו כי  . נוכל להשתמש בכך על מנת למצוא את התנגדות הקבל (נגד) הכדורי:
. נוכל להשתמש בכך על מנת למצוא את התנגדות הקבל (נגד) הכדורי:

אם נטען את הקליפות הכדוריות ב- המטען יזרום דרך ההתנגדות הכדורית:
המטען יזרום דרך ההתנגדות הכדורית:  , כאשר מתקיים כי
, כאשר מתקיים כי  .
.
תרגילים
שאלה
קליפה כדורית דקה מאוד ומבודדת שמרכזה בראשית הצירים, בעלת
רדיוס R טעונה בצפיפות משטחית המשתנה עם הזווית  (ביחס לציר z) לפי
(ביחס לציר z) לפי  . מהי העבודה שיש להשקיע כדי להעביר מטען נקודתי q מהנקודה
. מהי העבודה שיש להשקיע כדי להעביר מטען נקודתי q מהנקודה  אל הנקודה
אל הנקודה  ? (שתי הנקודות הינן מחוץ לקליפה).
? (שתי הנקודות הינן מחוץ לקליפה).
תשובה
חשוב לשים לב כי שתי הנקודות הן מחוץ לקליפה.
לפי חוק גאוס, מספיק שאנו במרחק  מהקליפה, אנו יכולים להתייחס אליה כאל מטען נקודתי.
מהקליפה, אנו יכולים להתייחס אליה כאל מטען נקודתי.
|
נראה שתי גישות לפתרון.
גישה אחת היא הליכה במסלול כזה הנראה בשרטוט:
אנו יכולים להתייחס אל הקליפה כאל מטען נקודתי.
המטען הכולל בתוך הקליפה הוא אפס. לפי גאוס  . .
|

|
שימו לב: ע"פ חוק גאוס ניתן להמיר את הבעיה,
כאשר דנים מחוץ לקליפת הכדור ב-![plot:\[dr\]](/documentResources/163/plot_2.png) לפחות, לבעיה של מטען נקודתי
שלא משנה מה ערכו לצורך הדיון (נניח
לפחות, לבעיה של מטען נקודתי
שלא משנה מה ערכו לצורך הדיון (נניח ![plot:\[q\]](/documentResources/163/plot_3.png) ). השדה של הבעיה החדשה הוא
). השדה של הבעיה החדשה הוא ![plot:\[\bar E = \frac{q}{{{r^2}}}\hat r\]](/documentResources/163/plot_4.png) והפוטנציאל
והפוטנציאל ![plot:\[V = \frac{q}{r}\]](/documentResources/163/plot_5.png) . אנו יכולים לדון רק בנקודות שמחוץ למעטפת הכדור.
הסימטריה היא רדיאלית שכן אנו דנים במטען נקודתי. במסלול שתואר עוברים לאורך כל
הדרך בפוטנציאל זהה ועל כן העבודה אפס.
. אנו יכולים לדון רק בנקודות שמחוץ למעטפת הכדור.
הסימטריה היא רדיאלית שכן אנו דנים במטען נקודתי. במסלול שתואר עוברים לאורך כל
הדרך בפוטנציאל זהה ועל כן העבודה אפס.
|
נוכל גם לבצע את המסלול הבא בין הנקודות:
בכל נקודה בתוך המעטפת נוכל להגדיר מעטפת גאוסית, אשר
המטען בתוכה הוא אפס. לכן גם השדה בכל נקודה בתוך הקליפה הינו אפס, ולכן
הפוטנציאל קבוע.
שוב, בחוץ פוטנציאל קבוע, ולכן הפרש הפוטנציאלים הוא אפס.
הסבר נוסף: נצייר את התפלגות המטען ונראה שהתפלגות המטען
כפי שהיא נראית משתי הנקודות היא זהה, כלומר, מתאמי סימטריה נוכל לומר
שהפוטנציאל בשתי הנקודות זהה, ולכן העבודה שיש להשקיע על מנת להעביר את המטען
בין הנקודות היא אפס.
|

|
שאלה
נתונות שלוש קליפות כדוריות מוליכות קונצנטריות בעלות
הרדיוסים R, 2R, 3R, הטעונות במטענים
q, -2q, 3q בהתאמה. מחברים את הקליפה החיצונית 3R אל הקליפה במרחק 2R
בחוט מוליך.
כמה מטען מצטבר על הקליפה ברדיוס 2R לאחר החיבור?
תשובה
|
כאשר אנו מחברים את הקליפה במרחק 2R עם הקליפה במרחק 3R
אנו יכולים להתייחס אליהן כאל קליפה אחת.
המטען q שעל הקליפה ברדיוס R מאלץ מטען –q על הקליפה במרחק 2R. כל שאר המטענים בורחים אל הקליפה השלישית, סה"כ מצטברים
על הקליפה הנמצאת במרחק 3R – 2q מטענים. |

|
שאלה
נגד בצורת קליפה כדורית בעלת רדיוס פנימי a ורדיוס
חיצוני b עשוי מחומר בעל מוליכות סגולית  בתחום
בתחום  ומוליכות סגולית
ומוליכות סגולית  עבור
עבור  .
.
א. חשב את התנגדות הנגד.
ב. מחברים את הנגד למקור מתח V. חשב את התנגדות הנגד בנקודה  .
.
תשובה א'
התנגדות נגד כדורי נתונה לנו על ידי:  כאשר a הוא הרדיוס הפנימי שלו ו-b הוא הרדיוס הפנימי.
כאשר a הוא הרדיוס הפנימי שלו ו-b הוא הרדיוס הפנימי.
הנגדים למעשה מחוברים בטור, ולכן נתחיל בחישוב ההתנגדות של
כל אחד מהם, ולאחר מכן הנגד השקול יהיה סכום ההתנגדויות.

תשובה ב'
נטען כי הזרם בחומר בעל המוליכות הסגולית  זהה לזרם הזורם בחומר בעל המוליכות הסגולית
זהה לזרם הזורם בחומר בעל המוליכות הסגולית  .
.
לפי חוק אום,  , כאשר V, R כבר נתונים לנו.
, כאשר V, R כבר נתונים לנו.
ידוע כי מוליכים המקיימים את חוק אום, מקיימים גם כי:  . כמו כן,
. כמו כן, 
אנו מתעניינים בצפיפות הזרם בנקודה b. לכן:  . המוליכות הסגולית בנקודה זו היא
. המוליכות הסגולית בנקודה זו היא  , ולכן:
, ולכן:



 בצורת גליל ישר, שטח חתך
בצורת גליל ישר, שטח חתך  ובעל אורך L.
ובעל אורך L. דרך שטח החתך A.
דרך שטח החתך A.

 .
. .
.
 זהו השטח שלה.
זהו השטח שלה.
 סוגים של נושאי מטען
סוגים של נושאי מטען  .
.

 הוא הממוצע של גודל פיסיקלי b:
הוא הממוצע של גודל פיסיקלי b: 

 משך הזמן עד ההתנגשות הבאה.
משך הזמן עד ההתנגשות הבאה.



 זוהי למעשה תכונה של החומר. נסמן:
זוהי למעשה תכונה של החומר. נסמן:  , ואז יתקיים כי:
, ואז יתקיים כי:  הפועל על נושא מטען אחד:
הפועל על נושא מטען אחד: (כוח כפול מהירות).
(כוח כפול מהירות). 

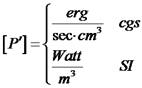







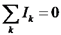
 המטען שעל הקבל,
המטען שעל הקבל,  הזרם במעגל.
הזרם במעגל. מתקיים:
מתקיים:  וכמו כן מתקיים כי
וכמו כן מתקיים כי  .
.  המפסק נסגר.
המפסק נסגר.





 .
.

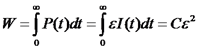



 קבוע כלשהו.
קבוע כלשהו.

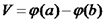 . נמצא את V בהתאם לנתוני השאלה:
. נמצא את V בהתאם לנתוני השאלה:


 . נוכל להשתמש בכך על מנת למצוא את התנגדות הקבל (נגד) הכדורי:
. נוכל להשתמש בכך על מנת למצוא את התנגדות הקבל (נגד) הכדורי:
 המטען יזרום דרך ההתנגדות הכדורית:
המטען יזרום דרך ההתנגדות הכדורית:  , כאשר מתקיים כי
, כאשר מתקיים כי  .
. (ביחס לציר z) לפי
(ביחס לציר z) לפי  . מהי העבודה שיש להשקיע כדי להעביר מטען נקודתי q מהנקודה
. מהי העבודה שיש להשקיע כדי להעביר מטען נקודתי q מהנקודה  אל הנקודה
אל הנקודה  ? (שתי הנקודות הינן מחוץ לקליפה).
? (שתי הנקודות הינן מחוץ לקליפה). מהקליפה, אנו יכולים להתייחס אליה כאל מטען נקודתי.
מהקליפה, אנו יכולים להתייחס אליה כאל מטען נקודתי.  .
. 
![plot:\[dr\]](/documentResources/163/plot_2.png) לפחות, לבעיה של מטען נקודתי
שלא משנה מה ערכו לצורך הדיון (נניח
לפחות, לבעיה של מטען נקודתי
שלא משנה מה ערכו לצורך הדיון (נניח ![plot:\[q\]](/documentResources/163/plot_3.png) ). השדה של הבעיה החדשה הוא
). השדה של הבעיה החדשה הוא ![plot:\[\bar E = \frac{q}{{{r^2}}}\hat r\]](/documentResources/163/plot_4.png) והפוטנציאל
והפוטנציאל ![plot:\[V = \frac{q}{r}\]](/documentResources/163/plot_5.png) . אנו יכולים לדון רק בנקודות שמחוץ למעטפת הכדור.
הסימטריה היא רדיאלית שכן אנו דנים במטען נקודתי. במסלול שתואר עוברים לאורך כל
הדרך בפוטנציאל זהה ועל כן העבודה אפס.
. אנו יכולים לדון רק בנקודות שמחוץ למעטפת הכדור.
הסימטריה היא רדיאלית שכן אנו דנים במטען נקודתי. במסלול שתואר עוברים לאורך כל
הדרך בפוטנציאל זהה ועל כן העבודה אפס.

 בתחום
בתחום  ומוליכות סגולית
ומוליכות סגולית  עבור
עבור  .
. .
.

 . המוליכות הסגולית בנקודה זו היא
. המוליכות הסגולית בנקודה זו היא 
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.