הרצאה 8 – אלקטרוסטטיות במוליכים ושיטת הדמויותאלקטרוסטטיות במוליכים (אידיאלים) מוליך אידיאלי זהו סוג של חומר, כך שתנועת מטענים בו נעשית ללא התנגדות. המטענים ישאפו לברוח אחד מהשני – יברחו לשפת הגוף. במוליכים אנו מקבלים מטענים רק על פני המוליך. בתוך מוליך, השדה החשמלי הוא
אפס, והמוליך הפוטנציאל החשמלי הוא קבוע (אחיד): על שפת המוליך קיים שדה חשמלי, הניצב לפני השטח: קיימת קפיצה ברכיב הניצב של השדה. על שפת המוליך נוצרת שכבת מטען בצפיפות ניקח גוף מתכת מוליך ללא מטען התחלתי, ונטען אותו במטען Q על ידי מגע. (המטען יתפזר על פני המוליך).
טעינה על ידי השראה חשמלית שלב א': מוליך שעל פניו שלב ב': נקרב אל המוליך מטען חיובי +Q. המטען החיובי יפעיל כוח על האלקטרונים החופשיים בגוף. המטען הכללי
שעל הגוף יישאר אפס. השדה
שלב ג': הארקה: נחבר את המוליך באמצעות תיל מוליך אל כלי קיבול חשמלי גדול מאוד.
המטען הכללי על השפה -Q. שדה חשמלי ליד קצה חד
המטען מתפזר על השפה. מודל: שני כדורים מוליכים, מחוברים ביניהם בתיל מוליך:
מכיוון שהכדורים מחוברים, הפוטנציאל בהם שווה. נניח כי התיל
המוליך אינו משפיע על התפלגות המטען בכדורים מתקיים: (2) הוא למעשה שיוויון בפוטנציאלים. מפתירת המשוואות נקבל:
מכאן, שהשדה על חוד יכול להיות עצום, וזאת אם דוגמא טעינה על ידי השראה של קליפה כדורית עבה ומוליכה. נשים מטען נקודתי
נבחר
נקבל בדיוק את אותה תוצאה אם נתאר את הבעיה בצורה הבאה:
סה"כ הקליפה נשארת נטרלית. אם נאריק את הקליפה, המטענים הטעונים +q יברחו, ונשאר עם קליפה טעונה במטען -q. נאמר כי המטענים +q הינם המטענים החופשיים של המערכת. כעת:
נבחר
שיטת הדמויות דוגמא תהי טבלה מוליכה מישורית אינסופית מוארקת, ויהי מטען נקודתי +Q במרחק h מהטבלה.
עבור תנאי השפה מתקיים: לכל לפי משפט היחידות הפתרון שמצאנו הוא הפתרון היחידי. כיצד מתפלג המטען המושרה?
לשדה הניצב קפיצה בשיעור צפיפות המטען המושרה ב צפיפות המטען הולכת וקטנה כש- כמות המטען הכללית המושרת היא Q. סיכום: השדה והפוטנציאל על כל נקודה במישור הם:
שיטת הדמויות - אלגוריתם רוטמן השימוש בשיטה כאשר יש התפלגות מטען שאיננו יודעים לחשב, אך את תנאי השפה של הפוטנציאל אנו יודעים לחשב. השיטה 1. מציאת תנאי השפה של הפוטנציאל. 2. מיקום מטען דמות במקום הצפיפות הבעייתית אשר מקיימת את תנאי השפה. 3. מציאת הפוטנציאל. 4. פתרון זה נכון רק עבור תחום הבעיה שבו נמצא המטען המקורי (האמיתי). הערה במבחנים תמיד מנסים להפיל את הסטודנטים על ידי השאלה מהי האנרגיה האלקטרוסטטית האגורה במערכת, בהתחשב בזה שהסטודנט הטיפש הממוצע ייחשב שדה עבור כל היקום בעוד השדה האמיתי הוא עבור חצי יקום בלבד.
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |



 .
. . מתקיים:
. מתקיים:  .
.
 .
. , והפוטנציאל
, והפוטנציאל  . עם זאת, התפלגות המטענים על הגוף תשתנה.
. עם זאת, התפלגות המטענים על הגוף תשתנה.



 .
.



 קטן בהרבה מ-
קטן בהרבה מ- .
. במרכז הקליפה.
במרכז הקליפה.

 .
.




 . הטבלה נשארה עם מטען שלילי.
. הטבלה נשארה עם מטען שלילי. (לא אחידה).
(לא אחידה). הוא יחיד.
הוא יחיד. .
.  ומ-
ומ- יתן אפס כאשר
יתן אפס כאשר  .
.  .
.
 , מתקיים:
, מתקיים:  (כמו קליפה מוליכה שנסגרת על עצמה ב-
(כמו קליפה מוליכה שנסגרת על עצמה ב- , השדה בפנים 0 והפוטנציאל נקבע לפי ההארכה ל-0. עבור
, השדה בפנים 0 והפוטנציאל נקבע לפי ההארכה ל-0. עבור  , מתקיים:
, מתקיים:  .
. (כלומר
(כלומר  ),
),  .
.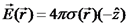 .
. במרחק r מנקודת ההיטל:
במרחק r מנקודת ההיטל:

 במעבר דרך התפלגות המטען המשטחית.
במעבר דרך התפלגות המטען המשטחית. :
: 
 ):
): 



תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.